You can find the source code for this file in the class repository. The direct link is here.

Model

Let’s start with studying static labor supply. We will consider the decision of the agent under the following rule:

\[ \max_{c,h} \frac{c^{1+\eta}}{1+\eta} - \beta \frac{h^{1+\gamma}}{1+\gamma}\\ \text{s.t. } c = \rho \cdot w\cdot h -r + \mu - \beta_0 \cdot 1[h>0] \\ \] The individual takes his wage \(w\) as given, he chooses hours of work \(h\) and consumption \(c\) subject to a given non labor income \(\mu\) as well as a tax regime defined by \(\rho,r\). \(\beta_0\) is a fixed cost associated with working. We ignore participation here, see the homework for including it.

We note already that the non labor income can control for dynamic labor supply since we can have \(\mu= b_t - (1+r)b_{t+1}\). This is part of a larger maximization problem where the agents choose optimaly \(b_t\) over time. We will get there next time.

Finding solution

The first order conditions give us \(w(wh +r - \mu)^\eta = \beta h^\gamma\). There is no closed-form but we can very quickly find an interior solution by using Newton maximization on the function \(f(x) = w(wh +r - \mu)^\eta - \beta h^\gamma\). We iterate on

\[x \leftarrow x - f(x)/f'(x).\]

# function which updates choice of hours using Newton step
# R here is total unearned income (including taxes when not working and all)
ff.newt <- function( x, w, R, eta, gamma, beta) {
  f0 = w*(w*x + R)^eta - beta*x^gamma
  f1 = eta*w^2 * (w*x + R)^(eta-1) - gamma * beta *x^(gamma-1)
  x  = x - f0/f1 
  # make sure we do not step out of bounds for next iteration
  x  = ifelse(w*x + R<=0, -R/w + 0.0001,x) 
  x  = ifelse(x<0, 0.0001,x)
  x
}

Simulating data with \(\beta=1\)

We are going to simulate a data set where agents will choose participation as well as the number of hours if they decide to work. To do that we will solve for the interior solution under a given tax rate and compare this to the option of no-work.

p  = list( eta = -1.5, gamma = 0.8, beta = 1, nu = 0.5 ) # define preferences
tx = list( rho = 1, r = 0 ) # define a simple tax
N=50000
simdata = data.table(i=1:N,X=rnorm(N))
simdata <- simdata[,lw := X     + rnorm(N)*0.2];      # add a wage which depends on X
simdata <- simdata[,mu := exp(0.3*X + rnorm(N)*0.2)]; # add non-labor income that also depends on X

# solve for the choice of hours and consumption
simdata <- simdata[, h := pmax(-mu+tx$r ,0)/exp(lw)+1] # starting value
# for loop for newton method (30 should be enough, it is fast)
for (i in 1:30) {
  simdata[, h := ff.newt(h, tx$rho*exp(lw), mu-tx$r, p$eta, p$gamma, p$beta) ]
}

# attach consumption, value of working
simdata <- simdata[, c  := tx$rho * exp(lw) * h + mu];
simdata <- simdata[, u1 := c^( 1 + p$eta )/( 1 + p$eta ) - p$beta * h^( 1 + p$gamma )/( 1 + p$gamma ) ];

At this point we can regress \(\log(w)\) on \(\log(c)\) and \(\log(h)\) and find precisely the parameters of labor supply:

pander(summary(simdata[,lm(lw ~ log(c) + log(h))]))
  Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.719e-15 1.454e-16 32.46 8.355e-229
log(c) 1.5 7.515e-17 1.996e+16 0
log(h) 0.8 1.424e-16 5.619e+15 0
Fitting linear model: lw ~ log(c) + log(h)
Observations Residual Std. Error \(R^2\) Adjusted \(R^2\)
50000 8.558e-15 1 1

The regression still works, among each individual who chooses to work, the FOC is still satisfied. To get the FOC we substitute \(c\) and take derivative with respect to \(h\) to get

\[ w_i c_i^\eta = \beta h_i^\gamma \] and taking logs, we get \[\log w_i + \eta log c_i = \log \beta + \gamma \log h_i\] - The regression is exact - The parameters when \(\beta=1\) are recovered

Heterogeneity in \(\beta\)

We introduce heterogeneity in the \(\beta\) parameter.

simdata <- simdata[,betai := exp(p$beta*X+rnorm(N)*0.1)] # TODO should be p$nu
simdata <- simdata[, h := pmax(-mu+tx$r ,0)/exp(lw)+1]
for (i in 1:30) {
  simdata <- simdata[, h := ff.newt(h,tx$rho*exp(lw),mu-tx$r,p$eta,p$gamma,betai) ]
}

# attach consumption
simdata <- simdata[, c  := exp(lw)*h + mu]; #TODO add rho

# let's check that the FOC holds
sfit = summary(simdata[,lm(lw ~ log(c) + log(h) + log(betai))])
expect_equivalent(sfit$r.squared,1)
expect_equivalent(coef(sfit)["log(c)",1],-p$eta)
expect_equivalent(coef(sfit)["log(h)",1],p$gamma)

# omitting betai doesn't work 
sfit2 = summary(simdata[,lm(lw ~ log(c) + log(h))])
expect_false(coef(sfit2)["log(c)",1]==-p$eta)

# finally we can try a natural regression since we don't observe betai directly:
sfit3 = summary(simdata[,lm(lw ~ log(c) + log(h) + X)])
pander(sfit3)
  Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.07648 0.001811 -42.24 0
log(c) 1.27 0.003119 407.3 0
log(h) 0.5768 0.001989 289.9 0
X 0.9382 0.001478 635 0
Fitting linear model: lw ~ log(c) + log(h) + X
Observations Residual Std. Error \(R^2\) Adjusted \(R^2\)
50000 0.08771 0.9926 0.9926

Simple case of \(\eta=0\)

In this case, the FOC is

\[ \log \rho + \log w = \gamma \log h + \nu x + \epsilon \] The question is whether we can run the regression to get the parameters. We run both wage on hours and hours on wage.

p  = list( eta = 0, gamma = 0.8, beta = 1, beta0 = 0, nu = 0.5) # define preferences
tx = list( rho=1, r = 0) # define a simple tax
N=500
simdata = data.table(i=1:N,X=rnorm(N))
simdata <- simdata[, lw    := X + rnorm(N) * 0.2];      # add a wage which depends on X
simdata <- simdata[, mu    := exp( 0.3 * X + rnorm(N) * 0.2)]; # add non-labor income that also depends on X
simdata <- simdata[, eps   := rnorm(N) * 0.1 ]
simdata <- simdata[, betai := exp( p$nu * X + eps )]
simdata <- simdata[, h     := ( tx$rho * exp(lw) / betai )^( 1 / p$gamma )]

sfit3 = summary(simdata[,lm(log(h) ~ lw + X)])
pander(sfit3)
  Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.0005792 0.005704 -0.1015 0.9192
lw 1.279 0.02917 43.85 5.924e-173
X -0.6523 0.02986 -21.84 1.21e-74
Fitting linear model: log(h) ~ lw + X Notice that we do get the correct coefficient here with
Observations Residual Std. Error \(R^2\) Adjusted \(R^2\)
500 0.1275 0.962 0.9619 
1/p$gamma
## [1] 1.25

On the other hand the reverse regression gives:

sfit4 = summary(simdata[,lm( lw ~ log(h) + X)])
pander(sfit4)
  Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0008373 0.003976 0.2106 0.8333
log(h) 0.6213 0.01417 43.85 5.924e-173
X 0.6112 0.009881 61.85 1.412e-235
Fitting linear model: lw ~ log(h) + X Which is quite different from the value of \(\gamma\).
Observations Residual Std. Error \(R^2\) Adjusted \(R^2\)
500 0.08888 0.9914 0.9914

We can use the correct estimate to construct a counter-factual revenue. We use directly that

\[ h_i = \left( \frac{\rho w_i}{\beta_i} \right)^\frac{1}{\gamma} \]

# we use our estimated parameters
p2  = list( eta=0, gamma = 1/sfit3$coefficients["lw","Estimate"], beta=1, beta0=0)
tx2 = tx
tx2$rho = 0.9

# we impute our counter factual errors
simdata <- simdata[, h2 := (tx2$rho*exp(lw)/betai)^(1/p2$gamma) ]

simdata[, list(
  totearnings =mean(h*exp(lw)), 
  R1=mean((1-tx$rho)*h*exp(lw)),
  R2=mean((1-tx2$rho)*h2*exp(lw)),
  R3=mean((1-tx2$rho)*h*exp(lw)) 
)]
##    totearnings R1        R2        R3
## 1:    3.478079  0 0.3110601 0.3478079
  • but did we know \(beta_i\) ?
  • is this unbiased?

Heterogeneity in \(\beta\) revisited

Finally we want to add heterogeneity in the \(\beta\) parameter.

Simulating

p  = list(eta=-1.5,gamma = 0.8,beta=1,beta0=0,nu=0.5) # define preferences
tx = list(rho=1,r=0) # define a simple tax
N=5000
simdata = data.table(i=1:N,X=rnorm(N))
simdata <- simdata[, lw := X     + rnorm(N)*0.2];      # add a wage which depends on X
simdata <- simdata[, mu := exp(0.3*X + rnorm(N)*0.2)]; # add non-labor income that also depends on X
simdata <- simdata[, eps := rnorm(N)]
simdata <- simdata[, betai := exp(p$nu*X+eps)]

#initial condition for h
simdata <- simdata[, h := (tx$rho*exp(lw)/betai)^(1/p$gamma)]
simdata <- simdata[, h := pmax(-mu+tx$r ,0)/exp(lw)+1]

for (i in 1:30) {
  simdata <- simdata[, h := ff.newt(h,tx$rho*exp(lw),mu-tx$r,p$eta,p$gamma,betai) ]
}

# attach consumption
simdata <- simdata[, c  := exp(lw)*h + mu];

# let's check that the FOC holds
sfit = summary(simdata[,lm(lw ~ log(c) + log(h) + log(betai))])
expect_equivalent(sfit$r.squared,1)
expect_equivalent(coef(sfit)["log(c)",1],-p$eta)
expect_equivalent(coef(sfit)["log(h)",1],p$gamma)

sfit2 = summary(simdata[,lm(lw ~ log(c) + log(h))])
expect_false(coef(sfit2)["log(c)",1]==-p$eta)

Biased and inconsistent regression

Wes start with the regression based on the first order condition:

\[\log w_i + \eta log c_i = \log \beta_i + \gamma \log h_i\]

and ignore the presence of unobserved \(\beta_i\).

pander(sfit2)
  Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.179 0.009033 -130.6 0
log(c) 1.771 0.00991 178.7 0
log(h) -0.4287 0.006084 -70.46 0
Fitting linear model: lw ~ log(c) + log(h)
Observations Residual Std. Error \(R^2\) Adjusted \(R^2\)
5000 0.3644 0.8704 0.8704 
ggplot(
    data.frame( 
      theta=c(-p$eta, p$gamma), 
      theta_hat= c( coef(sfit2)["log(c)",1], coef(sfit2)["log(h)",1] ),
      theta_sd= c( coef(sfit2)["log(c)",2], coef(sfit2)["log(h)",2] ),
      x=c('log(c)','log(h)') ), 
    aes(y=theta,x=x,er)) + 
  geom_bar(stat="identity",width=0.4,fill="blue",alpha=0.5) +
  geom_errorbar( aes(y=theta_hat, ymin= theta_hat - 1.96*theta_sd, ymax = theta_hat+ 1.96*theta_sd), width=0.1) + theme_bw() +
theme(text = element_text(size=20)) + xlab("regressors") + xlab("estimates")

IV condition

Next we have established the following condition in the class:

\[ E \left[ \log(w) - \gamma \log h - \eta \log c + \nu x | W,R,X \right] = 0 \] This suggests an IV strategy where we instrument using \(W,R,X\). We can use either hours or consumption as a dependent variable and instrument the other. We use \(h\) and implement using 2SLS (identical to IV in this case). We then first regress \(c\) on the three variables to get the predicted component, that we then use in a regression.

fit_c = simdata[, lm( log(c) ~ lw + log(mu) + X ) ]
simdata[, c_iv := predict(fit_c)]

sfit_iv2 = simdata[, lm( log(h) ~ c_iv + lw +  X   )]

pander(sfit_iv2)
Fitting linear model: log(h) ~ c_iv + lw + X
  Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.05263 0.05941 0.8859 0.3757
c_iv -1.958 0.1267 -15.45 1.24e-52
lw 1.308 0.0778 16.81 1.016e-61
X -0.6272 0.05757 -10.89 2.51e-27

Where we find as regression coefficients \(1/\gamma\) and \(\eta/\gamma\). Note of course that the inference out of the second regression is no valid (need to use IV formula, not only the second stage).

ggplot(
    data.frame( 
      theta=c(p$eta/p$gamma, 1/p$gamma, - p$nu / p$gamma), 
      theta_hat= sfit_iv2$coefficients[c('c_iv','lw','X')],
      x=c("c","w","x") ), 
    aes(y=theta_hat,x=x)) + 
  geom_bar(stat="identity",width=0.2,fill="blue",alpha=0.5) +
  geom_point(aes(y=theta),size=5) + theme_bw() +
  theme(text = element_text(size=20))  + 
  ylab("estimates") + xlab("regressors")

Heckman selection

We cover here a simple version of the Heckman selection. In the labor supply homework, you will see a version of this closer to the structure of the model presented at the beginning of this page.

We start with the following model:

\[ \begin{align} y_i^* & = \gamma x_i + \epsilon_i \\ d_i & = 1[ \delta_1 x_i + \delta_2 z_i + u_i \geq 0] \\ y_i & = d_i \cdot y_i^* \end{align} \] And only \((y_i, d_i, x_i, z_i)\) are observed. We assume that \((\epsilon_i,u_i)\) are jointly normal, mean zero and independent of \(x_i\).

Simulating

N=5000
p = list(gamma = 1.0, delta1 = 0.8, delta2 = 0.8, alpha = 1.0, sigma_v = 1.0, sigma_u = 1.0)
X = 2*runif(N)-1
Z = 2*runif(N)-1
U = p$sigma_u * rnorm(N)
D = p$delta1 * X + p$delta2 * Z + U >= 0 
E = p$alpha * U + p$sigma_v * rnorm(N)
Ys = p$gamma * X + E 

data = data.table(y = Ys * D, ys = Ys, d = D, x = X, z = Z, e = E, u = U)
data[ d==FALSE, y:=NA]

While \(E[ \epsilon_i | x_i ]=0\) we can’t use that for identification since what we observe is \((y_i, x_i)\) and not \((y^*_i, x_i)\), so we can’t construct \(E[ y^*_i x_i ]\).

We then need to rely on something else. We are going to look at \(E[ y^*_i x_i | d_i \geq 0 ]\) which is then equal to \(E[y_i x_i | d_i \geq 0 ]\) which is observed!

fit1 = lm(y ~ x,data)
pander(fit1)
Fitting linear model: y ~ x
  Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.7114 0.02585 27.53 5.942e-146
x 0.5954 0.04463 13.34 2.923e-39

We we compare the regression coefficient 0.5953532 to the true parameter 1. We can look at the distribution of the error.

ggplot(data[d==TRUE], aes(x = x, y= e)) + 
  geom_smooth() + 
  theme_bw() + 
  geom_hline(yintercept=0,linetype=2) +
  geom_smooth(data = data, label="unconditional", color="orange")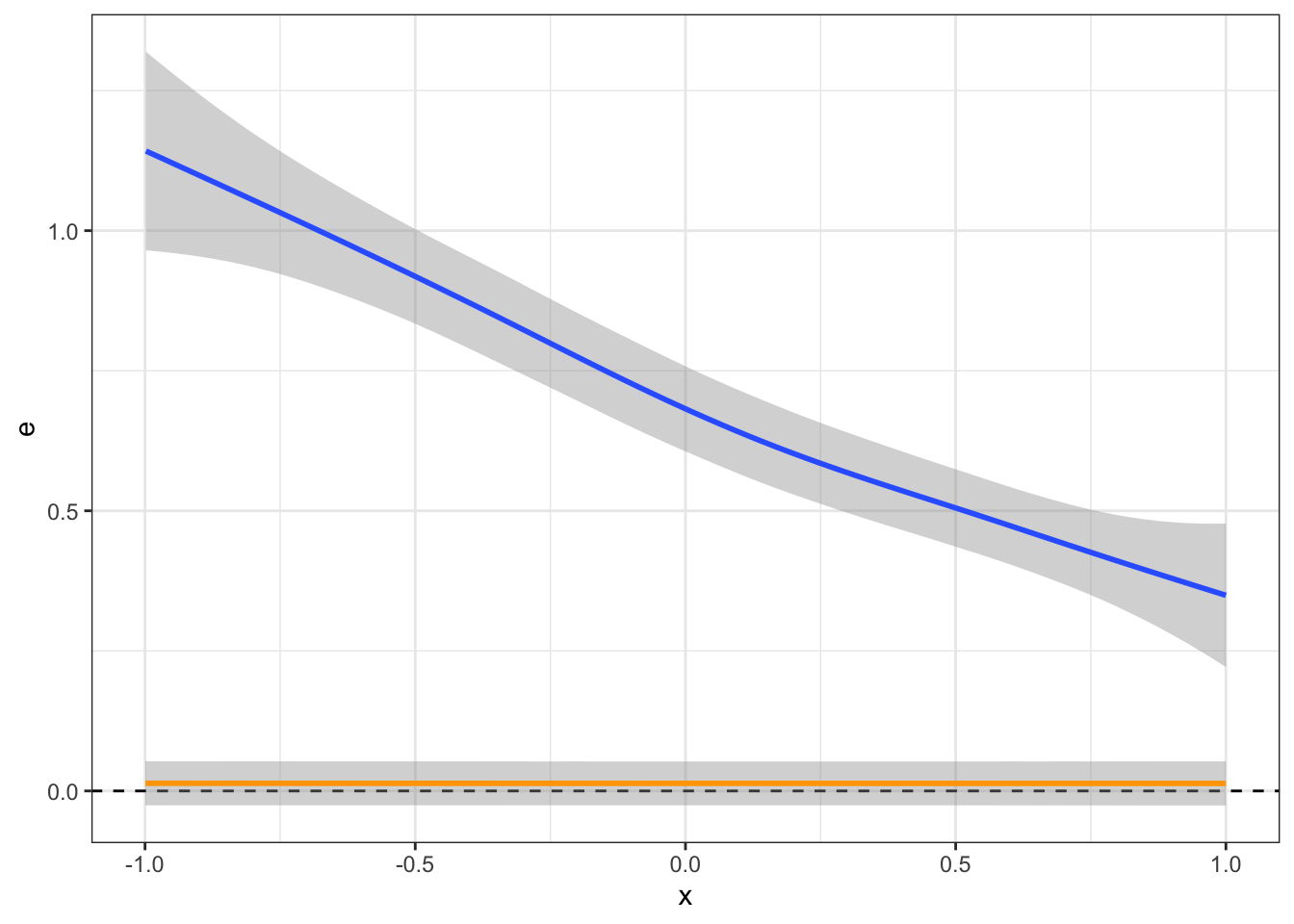

Deriving the correction

We then look at

\[ \begin{align} E[y_i | x_i, z_i, d_i=1 ] & = E[y^*_i | x_i, z_i, d_i=1 ] \\ & = E[\gamma x_i +\epsilon_i | x_i, z_i, d_i=1 ] \\ & = \gamma x_i + E[\epsilon_i | x_i, z_i, d_i=1 ] \\ \end{align} \] \((\epsilon_i,u_i)\) are jointly normal so we know we can write \(\epsilon_i = \alpha u_i + v_i\) where \(v_i\) is normal, mean zero and independent of \(u_i\). We can then write the conditional expectation as follows:

\[ \begin{align} E[\epsilon_i | x_i, z_i, d_i =1 ] & =E[\epsilon_i | x_i, z_i, \delta_1 x_i + \delta_2 z_i + u_i \geq 0 ] \\ & =E[\alpha u_i + v_i | x_i, z_i, \delta_1 x_i + \delta_2 z_i + u_i \geq 0 ] \\ & = \alpha E[u_i | x_i, z_i, \delta_1 x_i + \delta_2 z_i + u_i \geq 0 ] \\ & \quad \quad \quad \quad + E[v_i | x_i, z_i, \delta_1 x_i + \delta_2 z_i + u_i \geq 0 ] \\ & = \alpha E[u_i | x_i, z_i, \delta_1 x_i + \delta_2 z_i + u_i \geq 0 ] + 0 \\ & = \alpha E[u_i | u_i \geq -\delta_2 z_i -\delta_1 x_i ] \\ \end{align} \] Finally, we note that \(u_i\) is a normal distribution with some variance \(\sigma^2_u\). And we want to compute the mean of that distribution conditional on being lower than some value.

We can look at that.

\[ \begin{align} E[u_i | u_i \geq a ] & = \int_a^{\infty} u f_{u>a}(u) du \\ & = \int_a^{\infty} u \frac{1}{1-\Phi(\frac{a}{\sigma_u})} \frac{1}{\sigma_u} \phi ( \frac{u}{\sigma_u}) du \\ & = \frac{1}{1-\Phi(\frac{a}{\sigma_u})} \int_a^{-\infty} u \frac{1}{\sigma_u \sqrt{2 \pi }} \exp ( - \frac{u^2}{2\sigma_u^2}) du \\ & = \frac{1}{1-\Phi(\frac{a}{\sigma_u})} \Big[ \frac{-\sigma_u}{ \sqrt{2 \pi}} \exp ( - \frac{u^2}{2\sigma_u^2}) \Big]^{\infty}_a \\ & = \sigma_u \frac{ \phi(\frac{a}{\sigma_u})}{1-\Phi(\frac{a}{\sigma_u})} \\ \end{align} \] And so we we have that

\[ \alpha E[u_i | u_i \geq -\delta_2 z_i -\delta_1 x_i] = \alpha \sigma_u \frac{ \phi(\frac{-\delta_2 z_i -\delta_1 x_i}{\sigma_u})}{1-\Phi(\frac{-\delta_2 z_i -\delta_1 x_i}{\sigma_u})} \]

Which means that we need a value for \(\frac{\delta_1}{\sigma_u}\) and \(\frac{\delta_2}{\sigma_u}\). Luckily the participation decision given by \(\delta_2 z_i + \delta_1 x_i + u_i \geq 0\) and so the probit regression of \(d_i\) on \(z_i\) and \(x_i\) gives precisely these coefficients!

Indeed

fit2 = glm(d ~ x + z, family = binomial('probit'), data)
pander(fit2)
Fitting generalized (binomial/probit) linear model: d ~ x + z
  Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.02252 0.01914 1.177 0.2393
x 0.824 0.03451 23.87 5.793e-126
z 0.846 0.03483 24.29 2.59e-130

We can then use this to reconstruct our inverse mills ratio. Note that we don’t actually now the coefficient in the front. We don’t need it though.

data[, ai := predict(fit2)]
data[, m := dnorm(ai)/pnorm(ai)]

ggplot(data[d==TRUE], aes(x = x, y= e)) + 
  geom_smooth(se=FALSE) + 
  geom_smooth(aes(y=m),color='red',se=FALSE) + 
  theme_bw() #+ geom_point()

Corrected regression

fit2 = lm(y ~ x + m,data)
stargazer(fit1,lm(y ~ x + m,data),type="html",column.labels=c("naive","corrected"))
Dependent variable:
y
naive corrected
(1) (2)
x 0.595*** 0.992***
(0.045) (0.058)
m 0.971***
(0.093)
Constant 0.711*** 0.010
(0.026) (0.072)
Observations 2,508 2,508
R2 0.066 0.106
Adjusted R2 0.066 0.105
Residual Std. Error 1.238 (df = 2506) 1.212 (df = 2505)
F Statistic 177.912*** (df = 1; 2506) 147.742*** (df = 2; 2505)
Note: p<0.1; p<0.05; p<0.01

We can see that the regression coefficient is close to it’s true value!