Lab on Normal means
29 September, 2020
library(futile.logger)
library(data.table)Normal means
We consider the simple model given by
\[ y_{it} = \alpha_i + \epsilon_{it} \]
For simplicity we consider the case where \(\epsilon_{it}\) is Normal iid. And we consider a discrete distribution for \(\alpha_i\) parametrized by \(\alpha_k , p_k\).
We then set our model and simulate data.
# we consider a discrete presentation of a normal distribution for alpha
# require(Ckmeans.1d.dp)
# nk = 10
# nr = 1e6
# x <- rnorm(nr)
# result <- Ckmeans.1d.dp(x,nk)
# model0 = list(eps_sd=1, p_k = tabulate(result$cluster)/nr, alpha_k = result$centers)
#
# # simulate data
# nn = 1000
# sdata = data.table(eta_i = sample.int(nk,nn,prob=model0$p_k,replace=TRUE))
# sdata[, alpha_i := model0$alpha_k[eta_i]]
# sdata[, y1 := alpha_i + model0$eps_sd * rnorm(.N)]
# sdata[, y2 := alpha_i + model0$eps_sd * rnorm(.N)]
model0 = list(eps_sd=1, alpha_sd=1.5)
# simulate data
nn = 50000
sdata = data.table(alpha_i = model0$alpha_sd * rnorm(nn))
sdata[, y1 := alpha_i + model0$eps_sd * rnorm(.N)]
sdata[, y2 := alpha_i + model0$eps_sd * rnorm(.N)]FE approach
Here we want to recover the \(\alpha_i\) within each individual. A natural estimator in this case is then the average.
sdata[, alpha_hat := 0.5*(y1+y2)]
sdata[,var(alpha_hat)]## [1] 2.731139RE approach
Here we want to recover the \(\alpha_i\) within each individual. A natural estimator in this case is then the average.
# initialize with some parameters
model = list(eps_sd=0.1,alpha_sd=0.1)
rr = data.frame()
for (rep in 1:15) {
# we compute the posererior porobabilities
s = 1/(1/model$alpha_sd^2 + 2/model$eps_sd^2)
sdata[, mu_i := s * (y1+y2)/model$eps_sd^2]
sdata[, alpha_i_draw := mu_i + sqrt(s) * rnorm(.N)]
model$eps_sd = sqrt(sdata[, 0.5*(var( y2 - alpha_i_draw) + var( y1 - alpha_i_draw) )])
model$alpha_sd = sqrt(sdata[, var(alpha_i_draw)])
flog.info("eps_sd=%4.4f eps_alpha=%4.4f",model$eps_sd,model$eps_sd)
rr = rbind(rr,data.frame(model))
}## INFO [2020-09-29 19:07:00] eps_sd=0.8982 eps_alpha=0.8982
## INFO [2020-09-29 19:07:00] eps_sd=0.9867 eps_alpha=0.9867
## INFO [2020-09-29 19:07:00] eps_sd=1.0045 eps_alpha=1.0045
## INFO [2020-09-29 19:07:00] eps_sd=1.0050 eps_alpha=1.0050
## INFO [2020-09-29 19:07:00] eps_sd=1.0000 eps_alpha=1.0000
## INFO [2020-09-29 19:07:00] eps_sd=1.0006 eps_alpha=1.0006
## INFO [2020-09-29 19:07:00] eps_sd=1.0005 eps_alpha=1.0005
## INFO [2020-09-29 19:07:00] eps_sd=0.9980 eps_alpha=0.9980
## INFO [2020-09-29 19:07:00] eps_sd=1.0007 eps_alpha=1.0007
## INFO [2020-09-29 19:07:00] eps_sd=1.0011 eps_alpha=1.0011
## INFO [2020-09-29 19:07:00] eps_sd=0.9993 eps_alpha=0.9993
## INFO [2020-09-29 19:07:00] eps_sd=0.9992 eps_alpha=0.9992
## INFO [2020-09-29 19:07:00] eps_sd=1.0009 eps_alpha=1.0009
## INFO [2020-09-29 19:07:00] eps_sd=1.0020 eps_alpha=1.0020
## INFO [2020-09-29 19:07:00] eps_sd=1.0019 eps_alpha=1.0019rr$t=1:15
ggplot(rr,aes(x=t,y=eps_sd)) + geom_line() + theme_bw() + geom_line(aes(y=alpha_sd))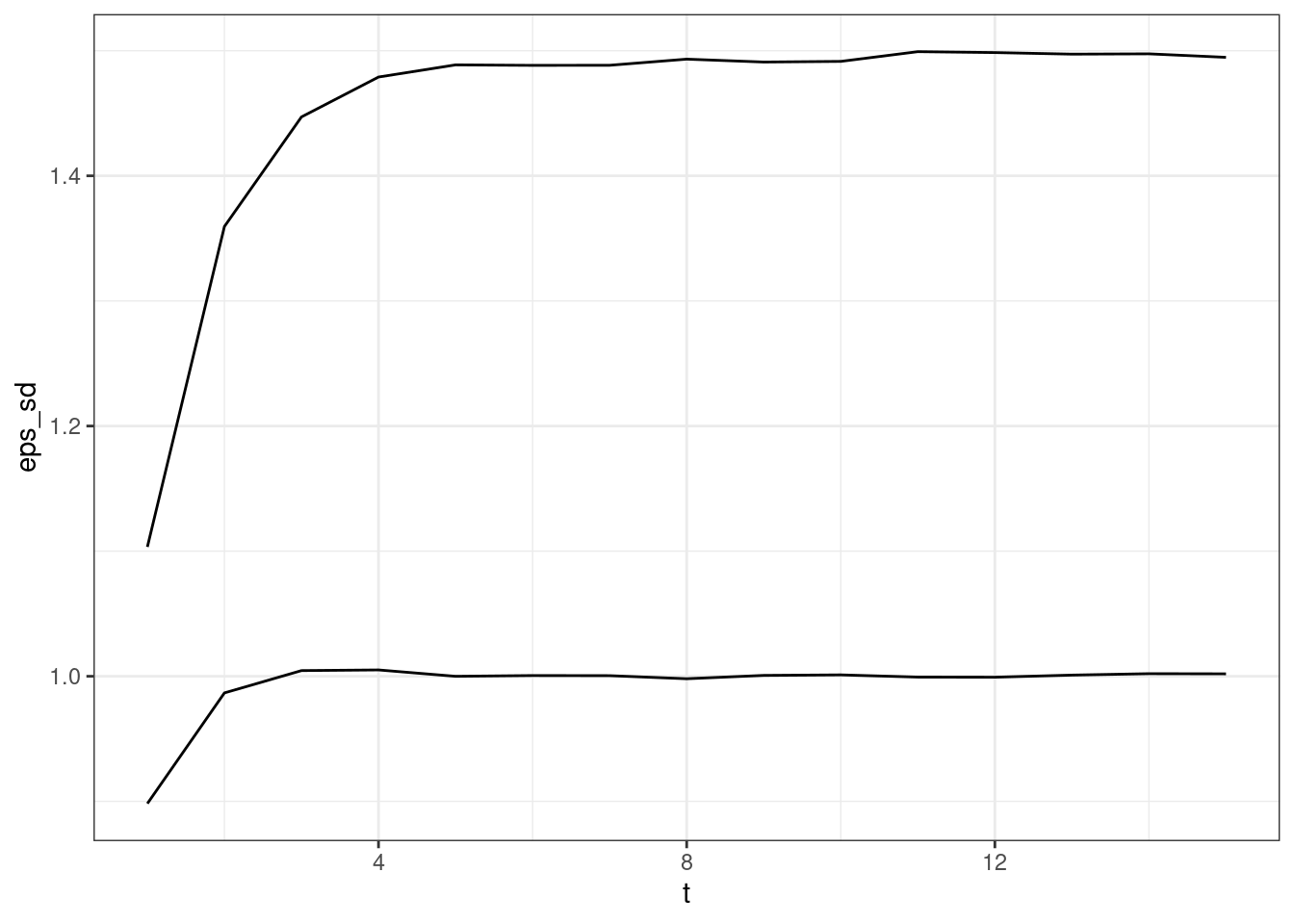
Variational approach
We now are going to also estaimate the posterior. Basically we estimate also a linear function for the mean and variance of the posterior.
# construct data with additional random draw
sdata[, eta_i := rnorm(.N)]
Y = c(sdata$eta_i)